Språkligt och historiskt betyder statistik sifferuppgifter om staten.

• Sifferuppgifter
  .. som beskriver en företeelse eller en verksamhet.
  
  
• Metoder
  .. för att samla in, bearbeta och analysera statistiskt material.

Oftast definieras statistik som vetenskapen om insamling, analys, tolkning och presentation av empiriska data. Statistiska metoder är mycket viktiga för insamling och analys av kvantitativa [stor mängd] data.

Det är viktigt att dina metoder för insamling och analys är effektiva för att minimera osäkerheten i beslutsprocessen.

Statistik används inom många områden t ex naturvetenskap, humaniora, politik och inom affärsvärlden. Enligt Statistiska institutionen på Ekonomihögskolan vid Lunds Univiesitet används statistitiska metoder inom alla områden av arbetslivet.

• Marknadsanalyser
  Förbättar kundnytta, kundservice och kunskap om olika behov.
  
  
• Tillverkningsindustrin
  Använder statistik i kvalitetsstyrningen.
  
  
• Arbetslöshet
  Statistiska metoder används för att mäta arbetslöshet.
  
  
• Läkemedelsindustrin
  Utvecklar nya läkemedel.
  
  
• Sjukvården
  Förbättrar behandlingsmetoder.

Resultatet av det material som samlats in, bearbetats och analyserats kallas även statistik. För att kunna kommunicera ditt resultat måste dessa stora mängder kvantitativa data presenteras på ett smart sätt.

Statistik, presenteras ofta i numerisk form i absoluta tal, frekvenstal, proportionerade tal eller som medeltal. Datan presenteras oftast i tabeller med tidsserier eller med andra jämförelsetal och illustreras ofta även i diagram eller figurer.

Det är viktigt att du är källkritisk till alla typer av statistik. Statistik kan, om den används okritiskt, ge dig en felaktig bild av verkligheten. Det finns ett "felaktigt" uttryck som lite lustigt beskriver detta.

"Lögn, förbannad lögn, statistik"
- Benjamin Disraeli, 1804-1881, författare & politiker

Spridningsmått är ett sammanfattande mått på utspridningen av värden som observerats eller en sannolikhetsfördelning.

När du räknat fram ett centralmått vill du veta hur mätvärdena fördelar sig runt detta centralmått. Ligger dina värden nära centralmåttet eller ligger de utspridda.

Ju mindre spridning desto bättre ur ett statistisk perspektiv. Det innebär att alla värden som observerats samlat sig närmare runt ett specifikt värde.

Vanliga spridningsmått är,

• Variationsbredd.
• Kvartil & percentil.
• Standardavvikelse.
  

Variationsbredd är ett mått som används för att beräkna spridningen i en serie observationsvärden. Det definieras som skillnaden mellan det högsta och det lägsta observationsvärdet i serien, d v s det högsta och lägsta mätvärde du har funnit.

Nackdelen med variationsbredd är att det inte tar hänsyn till alla värden, utan enbart det största och det minsta värdet. Det finns andra mått som ger en bättre bild av spridningen. I de flesta fall är det bättre att ange den nedre och övre kvartilen framför variationsbredden.

Variationsbredd
= störst värde − minst värde.

Exempel
11, 13, 16, 16, 18, 19, 21, 22, 22, 24, 31, 40.

Variationsbredd
= störst värde − minst värde.
= 40 − 11.
= 29.

Exempel
På senaste årsstämman fanns aktieägare närvarande i åldrarna mellan 2 år och 98 år.

Variationsbredd
= störst värde − minst värde.
= 98 år − 2 år.
= 96 år.

För att beskriva spridningen i en variabel kan du använda andra värden än det mittersta. Kvartiler är ett mått att bättre beskriva spridningen runt medianen. En kvartil betyder fjärdedel och erhålls genom att dela in observationsvärden , uppställda i storleksordning, i fyra lika stora grupper med hjälp av tre värden, Det finns tre olika kvartiler.

• Q1 = nedre kvartilen.
• Q2 = medianen.
• Q3 = övre kvartilen.

Kvartilavståndet
= övre kvartilen − nedre kvartilen.

Din population består av 19 observationer sorterade på den variabel du är intresserad av med lägst värde först. Femte värdet blir 1:a kvartilen, tionde värdet 2:a kvartilen och det femtonde värdet den 3:e kvartilen.

Kvartilerna är markerade med fet stil.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19.

• Q1 = nedre kvartilen = 5.
• Q2 = medianen = 10.
• Q3 = övre kvartilen = 15.
  
  Kvartilavstånd
  = övre kvartilen − nedre kvartilen.
  = 15 − 5.
  = 10.
  

Begreppet percentil innebär du använt en metod där materialet är indelat och sorterat i hundra lika stora delar där du sorterat observationerna från lägsta till högsta värde eller tvärtom.

En percentil är ett mätvärde som anger att x antal procent av dina observationer ligger under percentilen i fråga. Med 20-percentilen menas därför att 20 % av observationerna av variabeln har ett värde som är lägre än detta värde.

• P25 = 25-percentilen = Q1 = den nedre kvartilen.
• P50 = 50-percentilen = Q2 = medianen.
• P75 = 75-percentilen = Q3 = den övre kvartilen.
  

Det mest använda spridningsmåttet är standardavvikelsen. Det visar den genomsnittliga avvikelsen från medelvärdet i en serie observationer.

Standardavvikelsen
= beräknas i sex steg,

1. Beräkna medelvärdet.
2. Beräkna differensen av alla observationer och medelvärdet.
   
   
3. Beräkna kvadraterna på alla differenser i steg 2.
4. Addera ihop alla kvadrater i steg 3.
   
   
5. Dividera summan i steg 4 med 1 mindre än antalet värden.
6. Ta kvadratroten ur kvoten du fick fram i steg 5.
   

Kitty ska beräkna standardavvikelsen på längden på hennes säljsamtal. Torsdagen i vecka 47 ringde hon till utvalda kunder vid 7 tillfällen. Hennes samtal varade i 12 min, 19 min, 22 min, 17 min, 14 min, 23 min & 20 min.

Beäkna avvikelsen från medelvärdet för vart och ett av Kittys aktuella observationer. Använd dig av ovan angivna 6 steg.

1. Beräkna medelvärdet.
   = (12 + 19 + 22 + 17 + 14 + 23 + 20 ) ÷ 7 ggr.
   = 127 min ÷ 7 ggr.
   ≈ 18,14 min.
   
   
2. Beräkna differensen av alla observationer och medelvärdet.
   = (12 − 18,14) + (19 − 18,14) + (22 − 18,14) + (17 − 18,14) +
   (14 − 18,14) + (23 − 18,14) + (20 − 18,14).
   = − 6,14, 0,86, 3,86, 1,14, 4,14, 4,86 & 1,86.
   
   
3. Beräkna kvadraterna på alla differenser i steg 2.
   = (− 6,14)^2, (0,86)^2, (3,86)^2, (1,14)^2, (4,14)^2,
   ( 4,86)^2 & (1,86)^2.
   = − 37,7, 0,74, 14,9, 1,3, 17,14, 23,62 & 3,46.
   
   
4. Addera ihop alla kvadrater i steg 3.
   = − 37,7, 0,74, 14,9, 1,3, 17,14, 23,62 & 3,46.
   ≈ 98,86.
   
   
5. Dividera summan i steg 4 med 1 mindre än antalet värden.
   = 98,86 ÷ (7 − 1).
   ≈ 16,48.
   
   
6. Ta kvadratroten ur kvoten du fick fram i steg 5.
   = √ 16,48.
   ≈ 4,12.
   
   svar
   Standardavvikelsen är 4,12 minuter.
   Kittys samtal ligger i intervallet 18,14 min ± 4,12 min.
   

Kitty kan även beräkna standardavvikelsen med hjälp av en färdig formel.

Standardavvikelsen
= √ ∑(x−x̄)^ 2÷ (n-1).

Lådagram eller boxplot är ett diagram där statistiskt material åskådliggörs i form av en låda, som rymmer den mittersta hälften av materialet. Det innebär att "lådans" gränser blir den nedre och den övre kvartilen.

Den vanligaste varianten sammanfattar materialet med hjälp av fem värden,

• Lägsta värdet.
• Nedre kvartilen.
• Medianvärdet.
• Övre kvartilen.
• Högsta värdet.
  

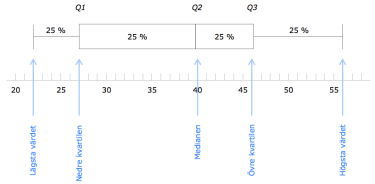
Nedan lådagram visar antal säljsamtal för Ursula Petzon under 23 dagar i mars 20x1. Nedan har vi presenterat observationsvärdena för Ursulas säljsamtal i ett lådagram.

Uppmätta värden [antal säljsamtal],

22, 22, 23, 24, 25, 27, 31, 34, 36, 37, 38, 40,
41, 41, 42, 42, 42, 46, 47, 48, 49, 55, 56.

• Lägsta värdet = 22 st.
• Nedre kvartilen = 27 st.
• Medianvärdet = 40 st.
• Övre kvartilen = 46 st.
• Högsta värdet = 56 st.
  
  
  Kvartilavståndet
  = Övre kvartilen − nedre kvartilen.
  = 46 st − 27 st.
  = 19 st.
  

Lägesmått är ett sammanfattande mått på "det genomsnittliga" värdet av observerade data eller en sannolikhetsfördelning. Det används för att sammanfatta, jämföra eller beskriva statistik. Lägesmått kallas även för genomsnittsmått.

Man kan t ex jämföra medelåldern i olika städer och utifrån det dra slutsatser om hur sjukvård och äldreboende bör planeras. Ett annat intressant område är hur många barn som föds. Då bör kommunerna planera och optimera antalet platser på kommunens förskolor.

Vanliga lägesmått är,

• Medelvärde.
• Median.
• Typvärde.
  

Medelvärde är ett lägesmått som visar ett genomsnittligt värde av ett urval eller en population. Det är ett värde som ungefärligt representerar en uppsättning värden.

Exempel
Under en vecka i mars har Alicia fikat på Café vid fem tillfällen. Hon har betalt 60 kr, 140 kr, 120 kr, 80 kr och 100 kr. Beräkna vad Alicia betalar för en fika i snitt.

• Exempel
  = (60 kr + 140 kr + 120 kr + 80 kr + 100 kr) ÷ 5 ggr.
  = 500 kr ÷ 5 ggr.
  = 100 kr per fika.

Medelvärde
= summan av värdena ÷ antal värde.

Molly driver ett litet konsultbolag. Varje tisdag eftermiddag ringer hon nya prospekts. Under 20x1 finns det 5 tisdagar i augusti. För att kunna bli en bättre säljare skriver Molly upp fakta om alla sina samtal. Beräkna medelvärdet av Mollys säljsamtal.

Medelvärde
= summan av värdena ÷ antal värde.
= (37 st + 43 st + 32 st + 42 st + 41 st) ÷ 5 tisdagar.
= 195 st ÷ 5 tisdagar.
= 39 samtal.

Median betyder "det värde som ligger i mitten". Du erhåller medianen genom att sortera alla värden i storleksordning och väljer därefter ut det värde som ligger i mitten.

• Exempel
  = 1, 2, 5, 6, 9, 11, 12, 19, 21, 21, 21, 24, 26.
  
  = −12, −8, −4, −2, 0, 2, 6, 7, 7, 9, 12, 18, 22.

För mängder med ett ojämnt antal tal är median det mittersta talet om de ordnas i storleksordning. För mängder med ett jämnt antal tal är medianen medelvärdet av de två mittersta talen.

Medianen kan i vissa fall ge en bättre bild av vad som är ”normalt” än vad ett medelvärde kan. Speciellt när antalet mätvärden är få och om de avviker mycket från övriga. Medianen tenderar att jämna ut effekterna av ett fåtal väldigt höga eller väldigt låga värden i en serie värden.

Median [fåtal observationer]
= det mittersta värdet av alla värden uppställda i storleksordning.

Median [många observationer]
= (n+1) ÷ 2.

Redovisa on line AB är en ny redovisningsbyrå som säljer webbrelaterade lösningar till verkstadsföretag i Norden. Pernilla som är företagets HR-chef har sammanställt nedan tabell. Beräkna medianen för företagets anställdas ålder.

Median
= det mittersta värdet av alla värden uppställda i storleksordning.
= 29 år; 37 år; 39 år; 45 år; 48 år; 55 år; 58 år; 60 år; 62 år.
= 48 år.

Typvärdet, som även kallas modalmått, är det värde som har den största frekvensen, d v s det vanligast förekommande talet i en grupp med värden.

Typvärde
= det vanligast förekommande talet i en grupp med tal.

Restaurang Hygget serverar sex olika lunchalternativ veckans alla dagar. Så här många gäster äter olika alternativ under en vecka, måndag-lördag. Beräkna typvärdet för att välja en viss sorts mat under veckans luncher.

Typvärde
= det vanligast förekommande talet i en grupp med tal.
= gästerna äter kött vid fyra tillfällen per vecka.
= 4.

Normalfördelning är en viktig fördelning inom sannolikhet och statistik. En normalfördelad variabel antar ofta värden som ligger nära medelvärdet och mycket sällan värden som har en stor avvikelse.

Ett statistiskt material där de flesta observationerna hamnar mycket nära medelvärdet. Fördelningen av observatinrtna ser likadant ut på båda sidorna över och under medelvärdet.

Normalfördelningen visas oftast som en normalfördelningskurva i ett klock-diagram. Den har alltid formen av en symmetrisk kulle eller puckel där den ena sidan ser likadan ut som den andra sidan

« statistik