"Matematiken är vetenskapens drottning"
- Carl Friedrich Gauss, 1777-1855, mattegeni extraordinaire
 
"Den högsta graden av ren tanke tänks i matematik"
- Platon, 427 f.Kr.-348 f.Kr, geni

vad är en investering?
i n v e s t e r i n g s k a l k y l e r i n g

En investering är en kapitalanvändning som får konsekvenser, på in- & utbetalningar, på lång sikt. Det finns dock många olika sätt att definiera en investering.

 

Det finns ettt antal olika sorters investeringar,

  • Materiella investeringar som t ex,
    - Fastigheter.
    - Maskiner.
    - Inventarier.

  • Finansiella investeringar som t ex,
    - Aktier.
    - Obligationer.
    - Övriga värdepapper.

  • Immateriella investeringar som t ex,
    - Varumärken.
    - Goodwill.
    - Patent.

 

Läs mer! vad är investering? - vad är en investering? »

Läs mer! olika exempel på investeringar - olika exempel på investeringar »

förenklingar i kalkylmodellen
i n v e s t e r i n g s k a l k y l e r i n g

En modell ska vara enkel att använda och enkel att förstå. För att kunna arbeta med invseteringskalkylering har vissa förenklingar [antaganden] gjorts.

 

  • Kalkyldatan anses säker.
  • Alla betalningar sker vid årsskiftet.
  • Stabilt penningvärde under hela investeringsperioden.

viktiga begrepp
i n v e s t e r i n g s k a l k y l e r i n g

Inom området investeringskalkylering finns några begrepp som är viktiga att kunna. När du lär dig dessa blir allt så mycket lättare.

 

  • Investering.
  • Investeringsbedömning.
  • Grundinvestering, G.

  • Restvärde, R.
  • Kalkylränta, r.
  • Inbetalningsöverskott, a.

  • Ekonomisk livslängd, n.
  • Pay Off [Pay Back].
  • Slutvärde

  • Nuvärde.
  • Internränta.
  • Annuitet.

 

Läs mer! begrepp, investeringskalkyl - begrepp, investeringskalkyl »

vad är kalkylränta?
i n v e s t e r i n g s k a l k y l e r i n g

Kalkylräntan återspeglar företagets krav på avkastning, d v s den diskonteringsränta som motsvarar investerarens avkastningskrav på kapital. Med hjälp av kalkylräntan kan du räkna ut nuvärdet för en enskild investering. Vid jämförelse mellan flera olika alternativ tillämpas samma kalkylränta.

 

Kalkylräntans två huvudsakliga funktioner är att användas,

  • Som företagets avkastningskrav.
  • Till att diskontera [omräkna] betalningar i tiden.

 

Det finns olika synsätt på vilken nivå kalkylränta du bör ha,

  • Alternativkostnaden för satsat kapital.
  • Vägt genomsnitt av ägares och låntagares förräntningskrav.

 

Företagets avkastningskrav [kalkylräntans storlek] ska ge en
avkastning som är större än,

  • Inflationen.
  • Risken.
  • En alternativ användning.

modell för investeringskalkyl
i n v e s t e r i n g s k a l k y l e r i n g

För att få en överblick över investeringens olika variabler kan du rita upp en enkel och pedagogisk modell. Den visar "GRran",

 

  • G
    Grundinvestering
    - investeringens ekonomiska värde vid start.

  • R
    Restvärde
    - investeringens ekonomiska värde vid utrangering.

  • r
    Kalkylränta
    - investeringens förväntade avkastning i %.

  • a
    Årligt inbetalningsöverskott
    - årliga inbetalningar - årliga utbetalningar.

  • n
    Ekonomisk livslängd
    - det antal år investeringen beräknas gälla.

 

Läs mer! modell för investeringskalkyl - modell för investeringskalkyl »

att välja metod
i n v e s t e r i n g s k a l k y l e r i n g

Vi har moderniserat Ljung & Högbergs matris från 1996. Den ställer de olika metoderna vid sidan om varandra för en bättre visualisering.

 

  • Pay back-metoden
    Ju kortare tid desto bättre.

  • Nuvärdemetoden
    Ju högre kapitalvärde desto bättre.

  • Annuitetsmetoden
    Ju högre annuitet desto bättre.

  • Internräntemetoden
    Ju högre internränta desto bättre.

 

Läs mer! val av metod - val av metod »

formler
i n v e s t e r i n g s k a l k y l e r i n g

Investeringskalkylering innebär att du multiplicerar en faktor med olika variabler beroende på vilken metod du valt att använda. Du beräknar olika faktorer,

 

  • Slutvärdefaktor.
  • Nuvärdefaktor.

  • Nusummefaktor.
  • Annuitetsfaktor.

 

Läs mer! formler - investeringskalkylering - formler - investeringskalkylering »

beräkna i spotlight
i n v e s t e r i n g s k a l k y l e r i n g

spotlight

Om du använder Mac kan du enkelt beräkna olika faktorvärde. Kopiera formeln, klistra in i spotligt och fyll i rätt siffror.

 

  • Slutvärdefaktor [tabell A]
    (1 + r)^n.

  • Nuvärdefaktor [tabell B]
    (1 + r)^-n.

  • Nusummefaktor [tabell C]
    (1- (1 + r)^-n) ÷ r.

  • Annuitesfaktor [tabell D]
    r ÷ (1- (1 + r)^-n.

 

Läs mer! beräkna i spotlight - beräkna i spotlight »

exempel, investeringskalkyl
i n v e s t e r i n g s k a l k y l e r i n g

 

 

Läs mer! pay back-metoden - pay back-metoden

Läs mer! nuvärdemetoden - nuvärdemetoden »

Läs mer! pay off, nuvärde, internränta- & annuitet - pay off, nuvärde, internränta- & annuitet »
 

träna på övningsuppgifter
i n v e s t e r i n g s k a l k y l e r i n g

För att lära dig investeringskalkylering krävs att du först läser teorin bakom. Därefter är det viktigt att du fördjupar dina kunskaper och färdigheter genom att träna på olika övningsuppgifter inom investeringskalkylering,

 

  • Pay back-metoden.
  • Nuvärdemetoden.

  • Annuitetsmetoden.
  • Internräntemetoden.

 

Läs mer! - övningsuppgifter & fullständiga facit övningsuppgifter & fullständiga facit »

pay back-metoden
i n v e s t e r i n g s k a l k y l e r i n g

Pay back-metoden är den enklaste investeringskalkylen och den som är mest intuitiv.

Pay back-metoden kallas även för pay off-metoden eller återbetalningsmetoden. Det är en metod som används för att beräkna hur snabbt en investering betalar sig själv, d v s hur lång tid det tar innan företaget tjänat in det investerade beloppet.

Hur lång tid det tar för de årliga inbetalningarna
= den ursprungliga utbetalningen.

 

Läs mer! pay back-metoden - pay back-metoden »

nuvärdemetoden
i n v e s t e r i n g s k a l k y l e r i n g

Med hjälp av kalkylräntan kan du räkna ut nuvärdet för en enskild investering. Vid jämförelse mellan flera olika alternativ tillämpas samma kalkylränta. Nuvärdet visar hur din investering klarar av avkastningskravet.

Nuvärdemetoden går ut på att beräkna hur framtida betalningar påverkar grundinvesteringen. För att kunna jämföra framtida betalningsströmmar med betalningar nu [idag], måste de diskonteras [räknas om] till ett värde idag, därav begreppet diskonteringsmetoden.

När du har summerat nuvärdet av alla framtida betalningar ska de jämföras med den ursprungliga grundinvesteringen. Det värde som räknas fram heter kapitalvärde, därav begreppet kapitalvärdemetoden.

 

Läs mer! nuvärdemetoden - nuvärdemetoden »

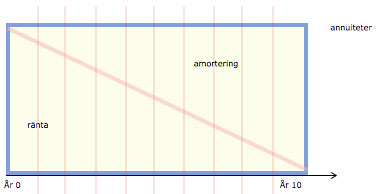
annuitetsmetoden
i n v e s t e r i n g s k a l k y l e r i n g

En annuitet är ett årligen återkommande lika stort värde som består av summan av en kapitaldel och en räntedel. Annuiteten i en kalkyl är alltid lika stor, men kapitaldelens och räntedelens inbördes förhållande förändras över tiden.

 

Du använder annuitet i stället för nuvärde när du ska,

  • Jämföra investeringar med olika livslängd.
  • Jämföra köpalternativ som sträcker sig långt fram i tiden med ett hyresalternativ som gäller årsvis.

 

annuiteter

 

Läs mer! annuitetsmetoden - annuitetsmetoden »

internräntemetoden
i n v e s t e r i n g s k a l k y l e r i n g

Med internräntemetoden ska du hitta investeringens maximala ränta, d v s den ränta där investeringens kapitalvärde är lika med noll.

Du söker investeringens nollpunkt med avseende på räntesats.

 

Läs mer! internräntemetoden - internräntemetoden »

så här använder du tabellerna

Vill du ha ett exakt svar ska du beräkna en faktor via dess formel. Vill du ha ett snabbt och ungefärligt svar ska du använda dig av tabeller.

 

  • Slutvärde
    = kapitalbelopp x slutvärdefaktor [tabell A].

  • Nuvärde
    = kapitalbelopp x nuvärdefaktor [tabell B].

 

Läs mer! så här använder du tabell A & tabell B - så här använder du tabell A & tabell B »

 

  • Nuvärdesumma
    = inbetalningsöverskott x nusummefaktor [tabell C].

  • Annuitet
    = årlig kapitalkostnad x annuitetsfaktor [tabell D].

 

Läs mer! så här använder du tabell C & tabell D - så här använder du tabell C & tabell D »

tabeller investeringskalkylering

Räntetabeller som hjälper dig att beräkna,

 

  • Slutvärdefaktor.
  • Nuvärdefaktor.

  • Nusummefaktor.
  • Annuitetsfaktor.

tabell A, slutvärdefaktor, svf
i n v e s t e r i n g s k a l k y l e r i n g

Slutvårdemetoden beräknar det årliga slutvärdet av en investering vid en angiven avkastning i procent.

 

Läs mer! tabell A, slutvärdefaktor - tabell A, slutvärdefaktor »

tabell B, nuvärdefaktor, nvf
i n v e s t e r i n g s k a l k y l e r i n g

Nuvärdemetoden [kapitalvärde- eller diskonteringsmetoden] "återför" alla in- och utbetalningar till tidpunkten för den urprungliga grundinvesteringen, d v s idag.

 

Läs mer! tabell B, nuvärdefaktor - tabell B, nuvärdefaktor »

tabell C, nusummefaktor, nsf
i n v e s t e r i n g s k a l k y l e r i n g

Nuvärdemetoden "återför" alla in- och utbetalningar till tidpunkten för den urprungliga grundinvesteringen, d v s idag.

 

Läs mer! tabell C, nusummefaktor - tabell C, nusummefaktor »

tabell D, annuitetsfaktor, af
i n v e s t e r i n g s k a l k y l e r i n g

Annuitetsmetoden fördelar grundinvesteringens utbetalning, inklusive ränta, med lika stora belopp varje år över investeringens ekonomiska livslängd.

 

Läs mer! tabell D, annuitetsfaktor - tabell D, annuitetsfaktor »

af = 1/nsf
i n v e s t e r i n g s k a l k y l e r i n g

Annuitetsfaktorn = 1÷ nusummefaktorn.

 

Enligt tabell C [nusumma] är nusummefaktorn [nsf] vid,

10 år och 10% ränta = 6,1446
15 år och 20% ränta = 4,6755
18 år och 12% ränta = 7,2497
25 år och 18% ränta = 5,4669

 

Enligt tabell D [annuitet] är annuitetsfaktorn [af] vid,

10 år och 10% ränta = 0,1628 = 1÷ nsf = 1÷ 6,1446
15 år och 20% ränta = 0,2139 = 1÷ nsf = 1÷ 4,6755
18 år och 12% ränta = 0,1379 = 1÷ nsf = 1÷ 7,2497
25 år och 18% ränta = 0,1829 = 1÷ nsf = 1÷ 5,4669

interpolera
i n v e s t e r i n g s k a l k y l e r i n g

Interpolering innebär att du använder dig av redan kända värden från t ex två kolumner i en tabell för att beräkna mellanliggande värden t ex ett värde mellan 4% och 6%.

 

  • Faktoruträkning med tabell kan ge ungefärliga värden.
  • Faktoruträkning med formel ger alltid korrekta värden

 

Läs mer! tabell, annuitetsfaktor - interpolera »
 
 

bidragskalkyl »

« investeringskalkyl

pålägg & marginal »
självkostnadskalkyl »

totalanalys »
 

övningsuppgifter »